Title: Structural Properties of Biochemical Systems Preventing Turing Instability
Authors: Minji Kang, Devanand, Jinsu Kim

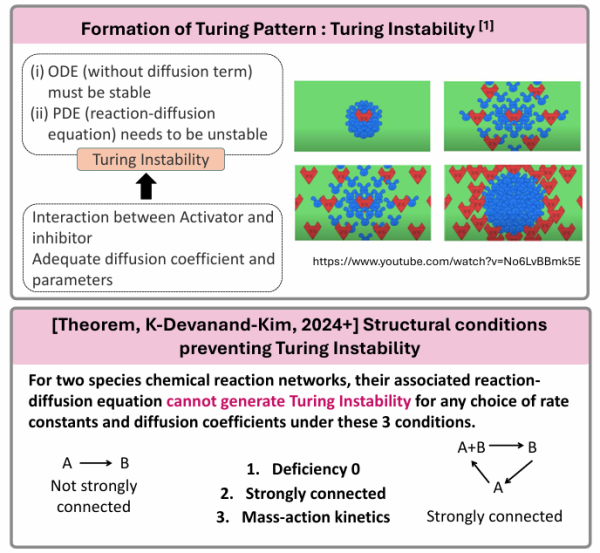
Biochemical systems are often represented graphically as reaction networks. In the study of these networks, a key focus is the relationship between their structural properties and their dynamic behavior. In this work, we explore reaction-diffusion equations where the reaction terms are governed by reaction networks with specific structural conditions. We show that for such networks, Turing instability cannot occur, regardless of the chosen reaction rates or diffusion coefficients.

This study aims to explain the formation of Turing Patterns using the structural properties of reaction networks. The formation of Turing Patterns depends significantly on parameters and diffusion coefficients, and in this work, we demonstrate that within certain conditions of Reaction Network Theory, Turing instability does not occur.