Mathematical data science and machine learning - through the lens of approximation theory
- Jae-Hun Jung
My primary research interests are centered around numerical analysis and scientific computing, with a specific focus on numerical partial differential equations (PDEs). Recently, my focus is also towards mathematical data science and machine learning, approached from an approximation perspective, particularly exploring topological data analysis within machine learning workflows.
In the field of numerical analysis, my research is in developing advanced theory for solving nonlinear hyperbolic conservation laws with non-smooth solutions. These conservation laws often lead to solutions that become discontinuous or non-smooth over time, despite having smooth initial conditions. This presents challenges as classical solutions might not exist, and obtaining accurate numerical solutions becomes complex. One notable issue is the Gibbs phenomenon, resulting in highly oscillatory numerical solutions when dealing with discontinuities. The research question is to create stable high-order methods to tackle such problems. A range of methods includes spectral methods, radial basis function methods, high-order finite difference/volume methods, and integrating artificial neural networks into machine learning workflows.
Traditionally, data analysis has heavily relied on statistical and probabilistic approaches. However, a recent mathematical theory, known as topological data analysis (TDA), has emerged, driven by the concept of persistent homology. This innovative approach offers a fresh perspective on data analysis by examining the shape of data. Instead of relying solely on statistical measures, TDA transforms data into geometric objects within metric spaces, investigating their topology using persistent homology. This method uncovers changes in the homological structures of data across different scales, revealing novel insights. Applications in machine learning workflows become also crucial, especially in graph neural networks. Despite promising results, challenges such as multi-parameter persistent homology, stability and structure theorem, and integration into machine learning workflows remain unsolved. My current research encompasses both the theoretical advancement of TDA and its practical applications. These applications range from diagnosing and predicting vascular diseases using TDA to detecting gravitational wave signals and even applying TDA to Korean music analysis and AI music composition.
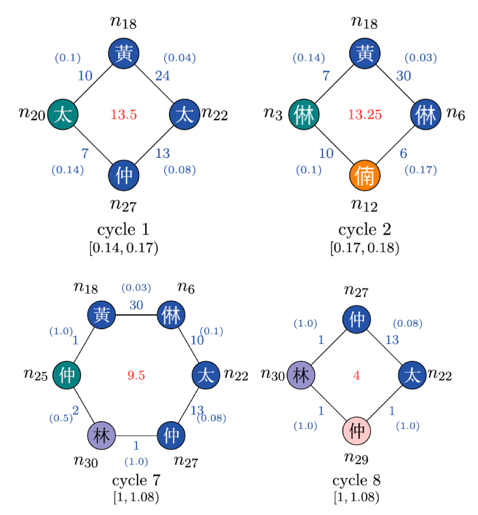
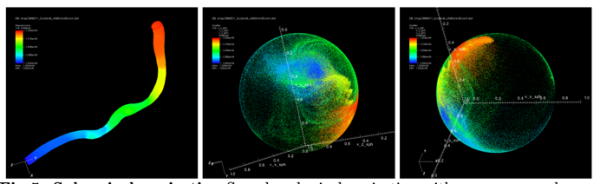
The figures below show some outcomes of the aforementioned research. The left figure illustrates cycles identified in a specific Korean music piece. Utilizing persistent homology, a novel music analysis approach has been developed, transforming music data into topological objects to reveal cyclic structures. This has led to the discovery of distinctive musical patterns embedded within Korean music. By training machines with these topological properties, a new piece of music, possessing topological similarities to the original, can be composed. On the right, the figure demonstrates the application of TDA to vascular flows. Given the significance of diagnosing and predicting vascular diseases, the concept of persistence from persistent homology proves valuable in quantifying disease severity. Lastly, we recently proved that TDA is quite useful in gravitational wave detection from black hole systems. This topological analysis introduces a fresh approach to detection, aiding in solving cosmological mysteries like the Hubble tension.
