My research area lies in the field of probability theory within mathematics, specifically, I am studying stochastic partial differential equations (SPDEs).  

SPDEs usually refer to partial differential equations (PDEs) perturbed by noise (random fields) where noise can be considered as random environment or random external force. While deterministic PDEs have been widely used to explain natural phenomena in the past, most natural phenomena are influenced by a random environment. Thus, currently SPDEs are widely used as models complementing deterministic PDEs in various fields such as physics, biology, finance, and climate. For instance, phenomena like the diffusion of plankton, which is influenced by random environments like solar radiation, ocean temperature, and salinity, can be modeled through SPDEs such as the parabolic Anderson model. Additionally, as seen when Martin Hairer received the Fields Medal in 2014 for his achievements in SPDEs, SPDEs are rapidly growing within the mathematics community.

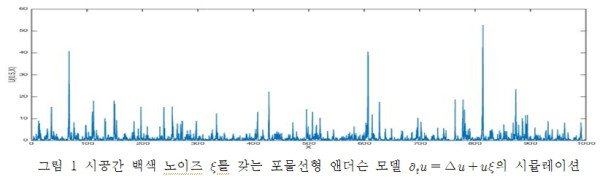
In my research on SPDEs, rather than focusing on the traditional research topics such as the existence and uniqueness of solutions, I am more concentrating on quantifying the characteristics of solutions that arise due to noise. For example, in the parabolic Anderson model driven by space-time white noise, the solution exhibits intermittency, which refers to the phenomenon that the solution shows tall peaks on some small regions and it is small between those peaks (see Figure 1 below).

This intermittency phenomenon does not occur without noise. In my research, I focus on the effect of noise on the long-time behavior of the solution, the geometric structure of tall peaks, the size between tall peaks, etc. Additionally, I investigate how the correlation structure of the noise affects the qualitative behaviors of solutions of SPDEs.