Kinetic Theory

Let's assume a sparse gas particle system (such as air, plasma, etc.), as we commonly envision. To simplify the system, we consider all particles to be extremely tiny spheres, and we assume that these particles undergo completely elastic collisions (conservation of mass, momentum, and energy) with each other. In this case, it is theoretically possible to describe the system by expressing the positions and velocities of each particle as functions of time using Newtonian mechanics.

However, in reality, there are too many particles in a gas. Therefore, to represent the gas particle system, we introduce a partial differential equation for the probability density function of the gas particles. The pioneering physicists who studied and researched this kind of probability density function were famous physicists, Maxwell and Boltzmann (as shown in the figure below). This field of research is also known as kinetic theory.

When we. Assume two particles have perfect elastic collision, the Botlzmann equation is written as

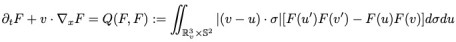
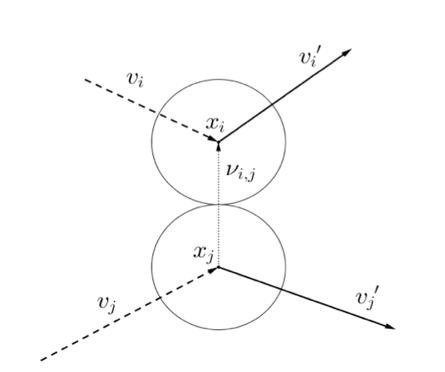
Where  is probability density function of rarefied gas at time, position, and. Velocity. u’ and v’ are post-collisional velocity from two particles with u and v (as shown in the figure below).

On the other hand, the Boltzmann equation or various equations in kinetic theory dealing with collisions and interactions satisfy the second law of thermodynamics, which is the entropy law in statistical physics. The entropy law is a fundamental principle in statistical physics that governs the equilibrium of a system. In kinetic theory, various equations describing gas particles are used as a basis to rigorously study macroscopic phenomena, such as the mathematical regularity of the system, analytical properties of solutions, and convergence to equilibrium states.

In this lab, we are studying the analytical and macroscopic phenomena of various kinetic equations in different situations, including boundary conditions. Additionally, ongoing research also includes the hydrodynamic limits obtained by scaling mean-free path which is related to fluid mechanics.