Qirui Li's research interests lie in Number Theory and Arithmetic Geometry

Qirui Li's research interests lie in Number Theory and Arithmetic Geometry.

Number Theory originated with the discovery of integers through counting, yet its essence extends far beyond initial appearances. For instance, an integer can define a mapping on the lattice 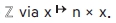In broader terms, for higher rank maps such as α: ℤ^n → ℤ^n, their eigenvalues, known as algebraic integers, embody a symmetry characterized by Galois groups. This symmetry is encapsulated in what are known as Galois representations.

These Galois representations are concealed within the cohomology of various spaces and curves, highlighting the significance of Arithmetic Geometry study.

Qirui's research delves into the interplay between analytic objects and diverse algebraic geometric entities emanating from lattices. A notable example is the Gross-Zagier formula, which correlates the central derivatives of L-functions with intersection numbers on Shimura varieties.

His Ph.D. thesis presented an intersection number formula for CM cycles in Lubin–Tate spaces, marking an early endeavor to address the linear Arithmetic Fundamental Lemma (linear AFL) for GLn. Subsequently, he and his collaborators expanded their focus to include different inner forms of GLn. Presently, he is exploring extensions of these theorems to local Shtukas, a functional field analogue of Shimura varieties. This exploration aids in investigating higher central derivatives of orbital integrals and L-functions.

Moving forward, Qirui aims to uncover deeper connections within Number Theory, especially surrounding the Guo–Jacquet Fundamental Lemma and its potential extensions to higher-dimensional groups like GLn.

Keywords: Number Theory, L-functions, Modular Forms, Elliptic Curves, Gross-Zagier Formula, Shimura Varieties, Shtukas, GL_n, Arithmetic Geometry.