Geometry of Fano varieties 

Algebraic geometry is a discipline that studies geometric objects known as algebraic varieties, which consist of solutions to systems of multivariable polynomial equations.

These geometric objects encompass familiar examples such as lines, planes, circles,conic sections (including ellipses and hyperbolas), as well as spheres, which we encounter during middle and high school education. Algebraic geometry has evolved alongside human civilization and has experienced rapid advancement from the 20th century to the present, playing a pivotal role in the development of modern mathematics.

Professor Jihun Park researches properties of algebraic varieties preserved by birational maps in algebraic geometry.

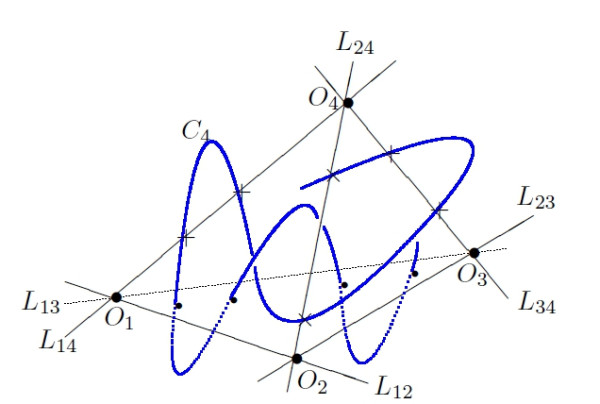
In particular, he focuses on varieties that play a fundamental role in the classification of algebraic varieties known as Fano varities. Over the past two decades,he has contributed to the advancement of algebraic geometry

through research on the following topics:

• singularities of Fano varieties

• groups of birational automorphisms of Fano varieties

• Non-rationality/rationality of Fano varieties

• K-stability of Fano varieties

• Einstein metrics on closed simply connected 5-dimensional manifolds

• cylindricity of Fano varities

In particular, since 2020, he has been focusing on the K-stability of smooth Fano 3-folds and

the existence problem of Einstein metrics on closed simply connected 5-dimensional manifolds.