My field of research lies at the intersection of differential geometry and the analysis of Partial Differential Equations (PDEs), an area broadly referred to as geometric analysis. Some fundamental questions in geometry and topology, such as the Calabi-Yau conjecture, the Riemannian Penrose inequality, the Poincaré conjecture, Thurston's geometrization conjecture, and the differentiable sphere theorem, often link topological information with the existence and rigidity of manifolds with special metric structures. The modern theory of PDEs and the calculus of variations have proven their efficacy in answering these questions, among many others. The resolutions of these problems are closely tied to milestone advances in geometric PDEs such as the complex Monge-Ampère equation, (inverse) mean curvature flow, Ricci flow, and the Einstein equations. These equations represent constraint equations of special geometric objects (here metric or submanifold) or deformations of these objects, potentially leading to convergence towards optimal structures.
In the actual study of these equations, it is natural and often unavoidable that the equations possess singularities, where regular solutions cease to exist. Although this
may initially appear unfavorable, it's actually a driving factor leading solutions to more desirable geometric structures. For instance, the proof of the Poincaré conjecture is based on the simple idea that Ricci flow on a 3-manifold simplifies and homogenizes its geometry, causing it to resemble simpler shapes like the sphere or cylinder at their singularities. A significant part of my research is devoted to studying the formation of singularities and the asymptotic behavior of solutions on small scales.The analysis of singularities typically involves three parts. Firstly, it's necessary to understand the convergence or compactness of blowing-up solutions, as this allows us to zoom into the behavior on smaller scales. Secondly, precise descriptions or classifications of such possible limits, known as singularity models, are obtained. Lastly, we look to understand the size and structure, distribution of the singular set using the results attained in previous steps.
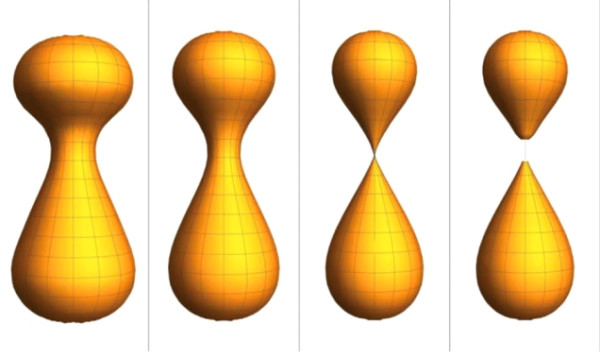
A Formation of neck-pinch singularity (at third from the left) in the Ricci flow, excerpted from [Alsing-Miller-Yau, A realization of Thurston’s geometrization: discrete Ricci flow with surgery, AMSA (2018)]
필요하시면 https://arxiv.org/pdf/1709.08494.pdf















.png)