VALENTIN BUCIUMAS: RESEARCH INTRODUCTION 

 Representation theory studies how algebraic objects like groups and Lie algebras act on vector spaces. When the vector spaces are finite-dimensional, the elements of the algebraic object act by matrices, which allows one to use linear algebra to study ‘non-linear’ objects. Developed at the end of the 19th century by Frobenius in order to study finite groups, it has then found several applications in physics and chemistry, particularly in quantum mechanics and the Standard Model, where Wigner noted that there is a connection between certain properties of elementary particles in a system and the structure of Lie groups related to the symmetries of the system. In this connection, states of the elementary particle correspond to an irreducible representation of the corresponding group.

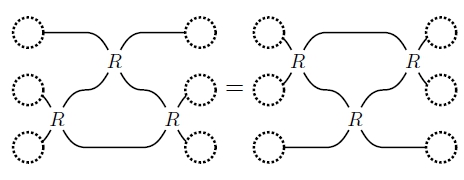
Figure 1. A pictorial representation of the Yang–Baxter equation.  

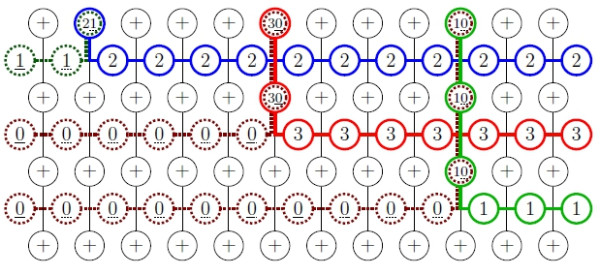
Figure 2. A state of an integrable system used to model metaplectic Whittaker functions.

The connection between representation theory and physics goes beyond applications of the former to the latter. The study of solvable lattice models (motivated by statistical physics) and the Yang–Baxter equation has led to the discovery of quantum groups by Drinfeld and Jimbo. Quantum groups are a fundamental object in modern representation theory, appearing in connection to a wide area of topics in mathematics, like knot invariants, categorification and special functions appearing in algebraic combinatorics and integrable probability.

 My own research focuses on the representation theory of p-adic groups, which can be thought of as number theoretic analogs of Lie groups. Many basic properties in this area, like explicitly determining the structure of Hecke algebras and studying associated Whittaker functions have led to a better understanding of the Langlands philosophy and had applications to the theory of automorphic forms and L-functions.

 Some of my research is driven by the desire to understand metaplectic covers of p-adic groups and p-adic loop groups, to which one may also meaningfully assign number theoretic objects like automorphic forms and Eisenstein series. Many difficulties arise in these settings of algebraic and combinatorial nature and I am especially fond of using techniques from the theory of quantum groups and integrable systems to tackle some of these problems.

 More info about my research can be found at buciumas.github.io.