확률 편미분 방정식

제 연구 분야는 수학 내에서 확률론이라 할 수 있고, 더 구체적으로는 확률 편미분 방정식(stochastic partial differential equation)을 연구하고 있습니다. 

확률 편미분 방정식은 일반적으로 편미분 방정식에 무작위적인 외부환경 혹은 외부 힘을 나타내는 노이즈가 추가된 방정식입니다. 과거에는 결정론적 편미분 방정식이 자연 현상을 수학적 모델로서 설명하는 데 널리 사용되었으나, 대부분의 자연현상은 무작위적인 외부 환경의 영향을 받기 때문에, 현재는 물리, 생물, 금융, 기후 등 다양한 분야에서 외부 환경을 노이즈로 표현하는 확률 편미분 방정식이 결정론적 편미분 방정식을 보완하는 모델로 사용되고 있습니다. 예컨대, 태양 복사, 바다의 온도, 염도 등 무작위적인 외부 환경에 영향을 받는 플랑크톤의 확산 작용과 같은 현상은 포물선형 앤더슨 모델과 같은 확률 편미분 방정식을 통해 모델링할 수 있습니다. 또한, 2014년에 마틴 헤어러 교수가 확률 편미분 방정식에 대한 업적으로 필즈상을 받은 것에서 알 수 있듯이 수학계 내에서도 확률 편미분 방정식의 위상이 매우 커지고 있습니다. 

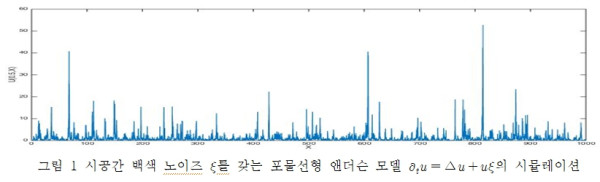
제 연구는 확률 편미분 방정식에서, 전통적 연구 주제인 해의 존재성과 유일성보다는, 노이즈로 인해 나타나는 해의 특성을 수학적으로 정량화하는데 초점을 두고 있습니다. 예를 들어, 시공간 백색 노이즈에 의해 유도되는 포물선형 앤더슨 모델에서는 해가 간헐성을 보이는데, 이는 아래 그림 1에서처럼, 해가 특정 지점에서 큰 값을 갖고, 그 사이에서는 0에 가까운 매우 작은 값을 갖는 현상을 말합니다.   

이러한 간헐성은 노이즈가 없을 때는 나타나지 않는 현상으로서, 제 연구는 노이즈의 영향으로 인해 시간 변화에 따라 해가 얼마나 큰 값을 갖는지, 큰 값을 갖는 공간의 기하학적 구조가 어떻게 되는 지, 피크들 사이에서 해가 얼마나 작은 값을 갖는 지, 그리고 그 공간의 크기는 어떻게 변화되는지 등을 연구하고 있습니다. 또한, 노이즈의 상관관계 구조가 해의 간헐성, 장기간 행동 같은 해의 정성적 특성에 어떠한 영향을 미치는지를 수학적으로 정량화하는 연구도 진행 중에 있습니다.