우리 연구실은 확률론과 이를 이용한 수리생물학을 주로 연구한다. 생명현상을 수학적으로 분석, 예측하는 분야인 수리생물학은 20여 년 전부터 큰 변화를 겪게 되는데, 이는 미시적 관점의 생명현상을 다루는 데 있어서 불확실성 (randomness)을 다루는 것 이 중요하다는 사실을 사람들이 인지하면서 시작된 변화이다. 이러한 변화로 인해 확률과정 (stochastic process)을 이용해 미시단위의 생명현상을 수학적으로 분석하는 연구가 주목을 받게 되었다.
여러 확률과정 중 우리 연구실은 주로 연속 시간 마르코프 체인을 다룬다. 마르코프 체인은, 마르코프 점프 프로세스라고 불리기도 하는데, 주로 세포 속 생화학 현상에 관여하는 개체들의 수를 시간에 따라 분석하기 위해 사용된다. 마르코프체인의 가장 큰 특징은 여러 반응 중 특정 반응이 다음에 일어날 확률이 과거의 상태가 아닌 정확히 현재의 상태로만 결정된다는 것이다. 세포 속 여러 생화학반응들이 현재 그 시스템에 속한 생화학 개체들의 개수에만 의존하여 변화가 일어난다는 가정을 할 수 있으므로 (물론 memory를 가지고 있는 생명현상도 많이 존재한다) 미시단위의 생명현상 속 개체들의 수를 분석하기 위해 마르코프체인이 많이 사용되고 있다.
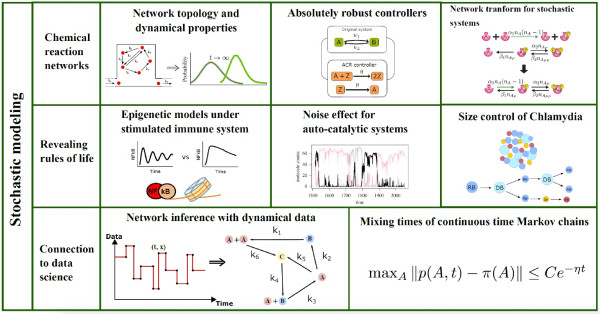
암 전이, 박테리아의 분화와 같은 특정 생명현상에 집중하여 그에 연관된 미해결 문제들을 수학적으로 분석하는 것이 수리생물학의 전반적인 흐름이라고 하면, 우리 연구실은 거꾸로 먼저 특정 수학적인 현상 (가령 마르코프 체인의 정성적인 특징인 안정성, 수렴성, 수렴 속도 등)을 어떤 생명현상이 만족하는지를 찾는 연구를 한다. 즉 어떤 화학반응 구조를 가진 생명현상이 수렴성을 가지는지, 그리고 언제 그 수렴이 기하급수적으로 일어나는지 등을 연구한다. 이를 전문적인 용어로 생화학 반응의 위상적 구조를 이용한 동역학적 특성 찾기라고 할 수 있다.
위에 언급한 연구를 체계적으로 진행하기 위해서는 생화학 반응들을 네트워크로 나타내어 그 네트워크의 구조적, 위상적 특징을 이용해 미분방정식이나 확률과정으로 분석하는 chemical reaction network 이론을 공부해야 한다. 1970년대 chemical reaction network의 위상적 성질 (node와 edge들의 개수나 연결성 등)이 그 네트워크 속 생화학반응으로 표현된 미분방정식의 안정성이나 수렴성을 입증하는데 큰 역할을 한다는 사실이 알려지면서 현재까지 미분방정식이나 마르코프체인의 정성적 특징과 네트워크의 위상적 특징을 연결하는 많은 연구가 진행되고 있다. Chemical reaction network는 현재 유럽이나 미국에서 수학자뿐 아니라 systems biology를 연구하시는 많은 분들이 사용하고 있는 방법론이다. 다만 네트워크를 통해 생명현상을 표현하는 연구에서 수학적으로 엄밀하지 않은 방식으로 접근하는 경우가 종종 있기에, 우리 연구실은 이러한 흐름을 개선하기 위해서 수학자뿐 아니라 타 분야의 학자들과 만나 서로의 분야에서 사용되는 언어와 개념들을 어느 정도 일치시키기 위한 노력을 하고 있다.
Chemical reaction network이론에서 더 나아가 마르코프 체인이나 확률 편미분 방정식과 연관된 확률론의 지식을 습득하여야 하고 있다. 특히 이미 밝혀진 마르코프 체인과 관련된 이론들은 주로 추상적이거나 혹은 특정 모델만이 만족시키는 조건들로 이루어진 경우가 많으므로, 우리는 단순히 기존의 이론을 적용하는 것을 넘어 마르코프 체인의 정성적인 움직임을 보장하는 새롭고 유용한 조건들을 찾는 연구를 진행하고 있다.
우리는 위에서 언급한 마르코프 체인의 동역학적 특징에 관한 연구를 이론적인 결과를 도출하는데 그치지 않고 그 이론적 결과를 활용하여 생명현상을 직접적으로 다루는 실용적인 연구도 진행하고 있다. 가령 기존의 생명현상에 생화학controller를 부착하여 원하는 결과를 얻는 데 있어서 마르코프 체인의 안정성을 이용할 수 있다. 또한 DNA의 움직임을 확률보행과 같은 마르코프 체인으로 표현하여 실제 실험으로 보기 힘든 특성을 찾는 연구도 진행했다. 현재에도 플라즈마 화학반응이나 액체 간 상전이 현상 등 확률론과 연관된 여러 생명현상을 연구하고 있다.
현재 수리생물학의 큰 흐름 중 하는 인공지능을 이용해 주어진 생명현상의 데이터 속 숨어있는 규칙을 찾고 이를 수리모델을 건설하여 분석하는 것이다. 우리 연구실은 이러한 흐름과는 반대로 인공지능을 이용해 생명현상을 분석하는 접근법이 아닌 생명현상에서 영감을 받은 새로운 계산과학 알고리즘을 만드는 새로운 연구를 추구하고 있다. 현재 생화학반응을 이용한 신경망 학습과정을 구현하는 연구를 진행하고 있는데, 이는 biology computing이라는 역사가 깊은 분야에 새로운 흐름을 줄 수 있는 연구가 될 수 있다.
우리 연구실의 여러 목표 중 하나는 Positive recurrence conjecture를 해결하는 것이다. 이는 “잘 연결된 생화학 반응은 안정적 이다” 라는 추측을 수학적으로 증명하는 것이다. 이와 같이 생명현상 전반을 아우르는 법칙을 수학적으로, 특히 확률론을 이용해 증명하는 것을 목표로 한다. 또 다른 목표는 물리학이 그러했듯이, 생명현상에서 기인한 확률론의 중요한 문제를 새로 정의하고 그것을 해결하는 것이다. 마지막으로 위에서 언급한 biology computing에 새로운 수학적 이론을 만드는 것 또한 장기적인 계획 중 하나이다.
우리 연구실의 학생들은 주로 마르코프 체인과 연관된 이론 문제와 확률론을 이용한 좀 더 실용적인 연구를 동시에 진행하고 있다. 전자를 위해서 확률론 관련 논문들을 읽고 발표하는 journal club을 매주 정기적으로 진행하고 있다. 또한 후자를 위해서 포스텍을 포함한 국내외 여러 연구소나 학교에 속한 생명, 의학 관련 연구자들과 공동 연구를 진행하고 있다. 공동 연구 및 다양한 분야 사람에게 자신의 연구를 알리는 것이 상대적으로 중요한 수리생물학이라는 분야 특성에 맞게 박사 과정 학생들에게 학위 과정 중 최소 6개월 이상은 해외의 연구소나 학교에 중장기 연구 방문하여 세계의 여러 수리생물학자 및 다양한 분야의 학자들과 연구 교류를 할 기회를 주고 있다.














.png)