이동현 교수
최고관리자
2024-07-11

키네틱 이론
우리 일반적으로 생각하는 희박한 기체 입자 시스템(예를 들면 공기, 플라즈마 등)을 가정해 보자. 시스템을 단순화 시키기 위해서 모든 입자가 아주 작은 공으로 되어있다고 생각하고 입자들이 서로 완전탄성충돌(질량, 운동량, 에너지 보존)을 한다고 가정하면 각 입자의 위치 및 속도를 시간의 함수로 표현하여 뉴턴 역학을 통해 시스템을 기술하는 것이 원칙적으로 가능하다.
하지만 현실적으로 기체에는 너무 많은 입자들이 존재한다. 따라서 기체 입자 시스템을 기체입자들의 확률밀도함수에 대한 편미분 방정식으로 표현하는데 이런 확률 밀도 함수를 도입하고 연구한 대표적인 학자들이 유명한 물리학자들인 막스웰과 볼츠만이다. (아래 그림) 또한 이러한 연구분야를 키네틱 이론이라고 부른다.

두 입자들이 완전 탄성 충돌한다는 가정할때 희박 기체 시스템을 표현하는 대표적인 방정식이 바로 볼츠만 방정식이다. 시간, 위치, 속도에 대한 확률밀도 함수를 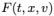 라고 가정하면 볼츠만 방정식은
라고 가정하면 볼츠만 방정식은
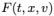 라고 가정하면 볼츠만 방정식은
라고 가정하면 볼츠만 방정식은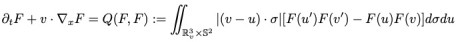
여기서 v’과 u’은 v와 u를 속도로 가지는 두 입자가 완전탄성 충돌한 이후의 각 입자의 속도이다. (아래 그림 참조)
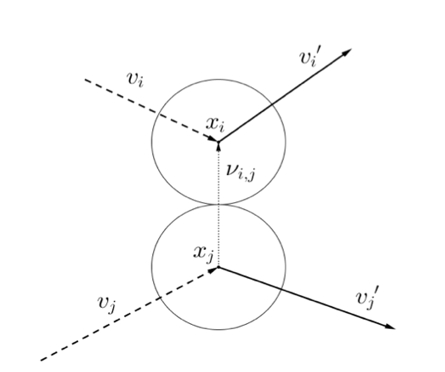
한편 위와 같은 볼츠만 방정식, 혹은 상호 충돌 및 영향을 다루는 키네틱 이론의 다양한 방정식들은 통계물리학의 열역학 2법칙인 엔트로피 법칙을 만족한다. 엔트로피 법칙은 통계물리학에서 시스템이 평형을 이루게 되는 근본원리로 알려져 있다. 키네틱 이론에서는 기체입자를 묘사하는 다양한 키네틱 이론의 방정식에 기반하여 시스템의 수학적 정칙성, 방정식해의 해석적 성질 및 평형상태로의 수렴과 같은 거시적인 현상을 수학적으로 엄밀하게 연구한다.
본 연구실에서는 경계조건을 포함한 다양한 상황에서 다양한 키네틱 방정식들의 해석적, 거시적 현상들에 대하여 연구한다. 또한 입자들의 충돌간 간격을 스케일링하여 얻는 유체역학한계(hydrodynamic limit)에 관련된 연구 또한 진행중이다.














.png)